机器学习

b站：BV1LR4y1R77n

进度：p20

一些概念：

特征标准化：通过公式将数据化为0~1之间

回归问题

1. 误差项定义

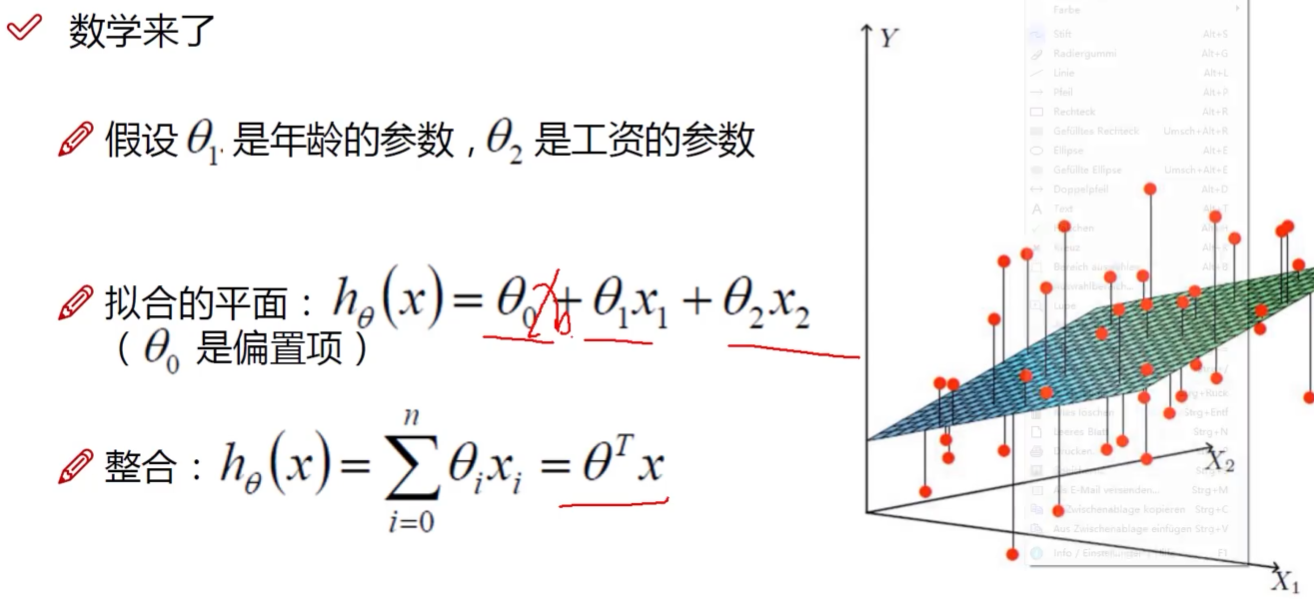
解释：

经常出现一列全为0的X自变量，这是为了起到一个占位的目的，比如上面的$X_{0}$

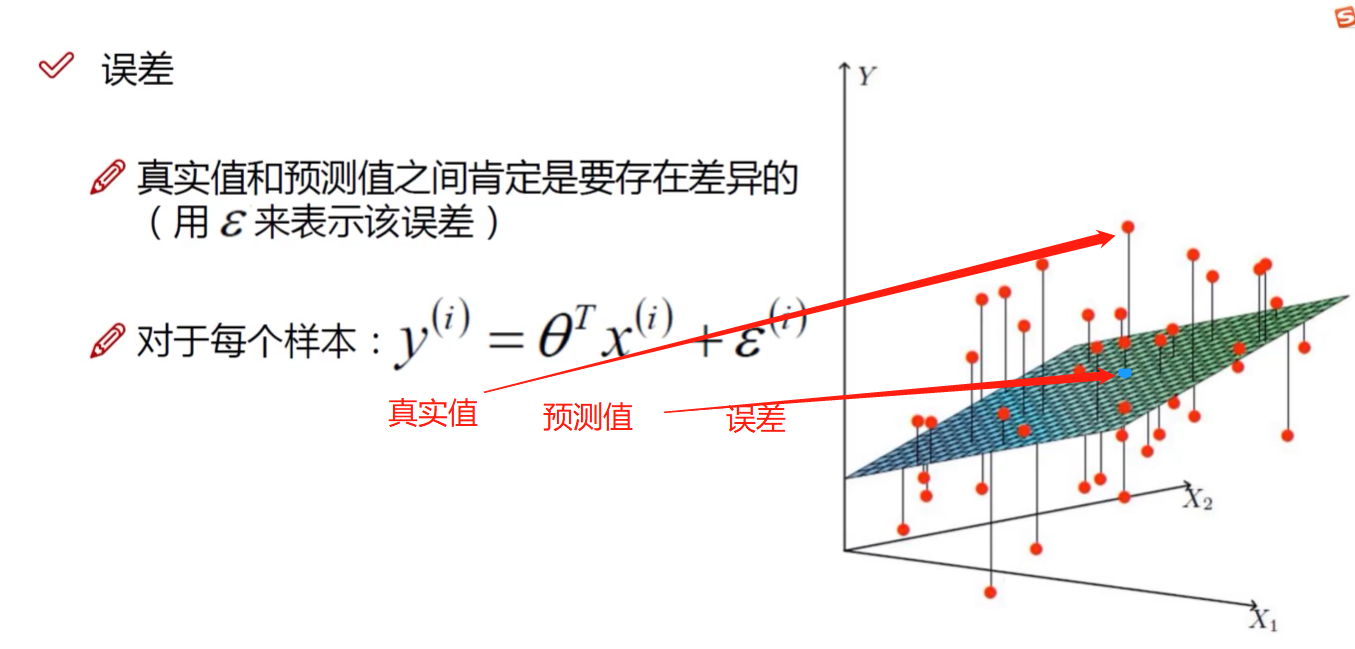
解释：

机器学习：你告诉机器一个目标，让机器去学习，我们要让这个误差更小

2. 独立同分布的意义

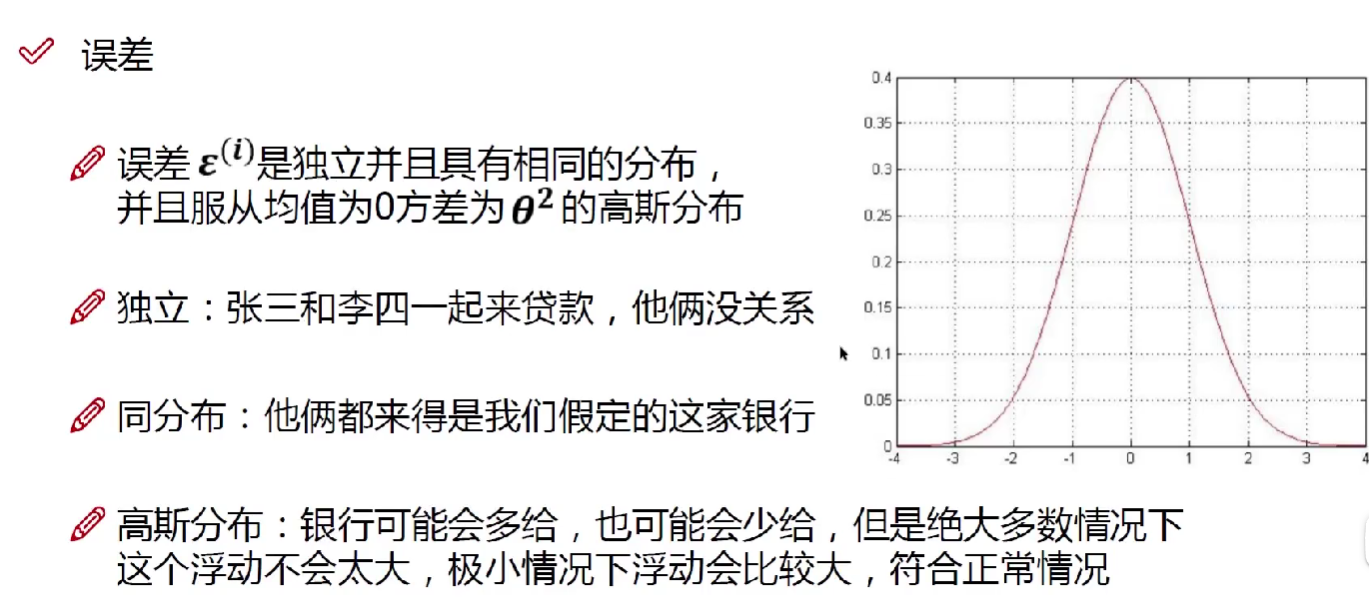
解释：

同分布：指训练集和测试集中的数据具有相同的概率分布。

独立：指的是一组随机变量之间相互独立或不存在相关性。

高斯分布=正态分布

独立同分布：相当于每次都同样调用一个计算概率的函数，产生不同的概率。

意义：确保模型的有效性和可靠性。

3. 似然函数的作用

似然函数是一种在统计学中常用的函数，用来描述已知一组数据后，参数取值的可能性大小。简而言之，似然函数是给定某些观察结果时，关于未知参数的函数。在概率论和统计学中，似然函数可以被用于估计最合适的参数，以便使得这组观察结果发生的概率最大。

解释：

（1）真实值=预测值+误差

让$\theta$与X结合后与y越接近越好

exp就是数学经常用到的那个e（约等于2.7那个）

似然函数的作用：

它可以用于寻找最优的参数取值，并进行模型比较和假设检验，因此被广泛应用于不同的领域和问题中。

具体来说，似然函数的作用可以从以下几个方面解释：
1. 参数估计：在已知一组数据的情况下，利用似然函数可以估计出最合适的参数取值，使得该组数据出现的概率最大。这种方法被称为最大似然估计，是常用的参数估计方法之一。
2. 模型比较：似然函数也可以用于比较不同的模型，来确定哪个模型更符合数据的分布。在模型比较中，我们通常会比较两个模型对应的似然函数大小，从而选择更合适的模型。
3. 假设检验：利用似然函数还可以进行假设检验，以判断某种假设是否成立。在假设检验中，我们通常会将给定的假设与一个备择假设进行比较，通过比较两者对应的似然函数大小，来决定是接受还是拒绝给定的假设。

似然函数越大越好，因为越大表明处于高斯函数越集中的位置,表明$(y^{(i)}-\theta^Tx{(i)})^2$越小，我们可以看一下高斯函数

其对称轴为$x=\mu$，表明，$x$越接近$\mu$，f(x)的值越大。所以反过来f(x)的值越大，表明$x$越接近$\mu$，也就是我们这个误差$(y^{(i)}-\theta^Tx{(i)})^2$越小

4. 参数求解

解释：

要想让似然函数越大，得让

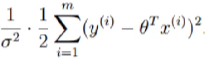
越小

5. 梯度下降

梯度下降是为了让$J(\theta)$取得最小值，从而使似然函数取得更大值

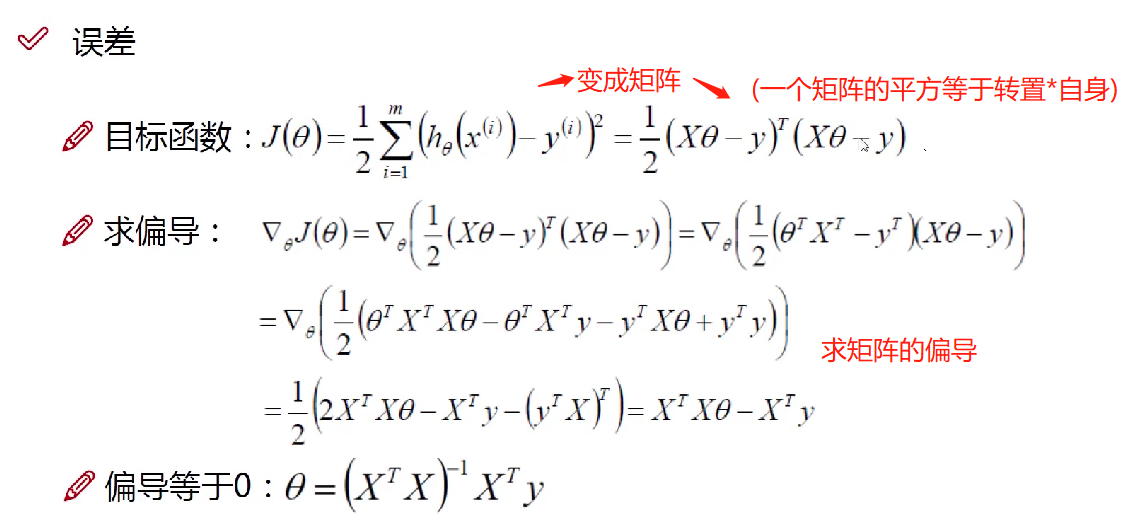
解释：要想求目标函数的最小值，我们要对目标函数进行求导，看一下最低点

解释：

目的：优化到损失值最小

解释：

x$^i_j$ i为第几样本，j为样本中的第几个变量
小批量梯度下降是前面两种的综合，一般取64次以上

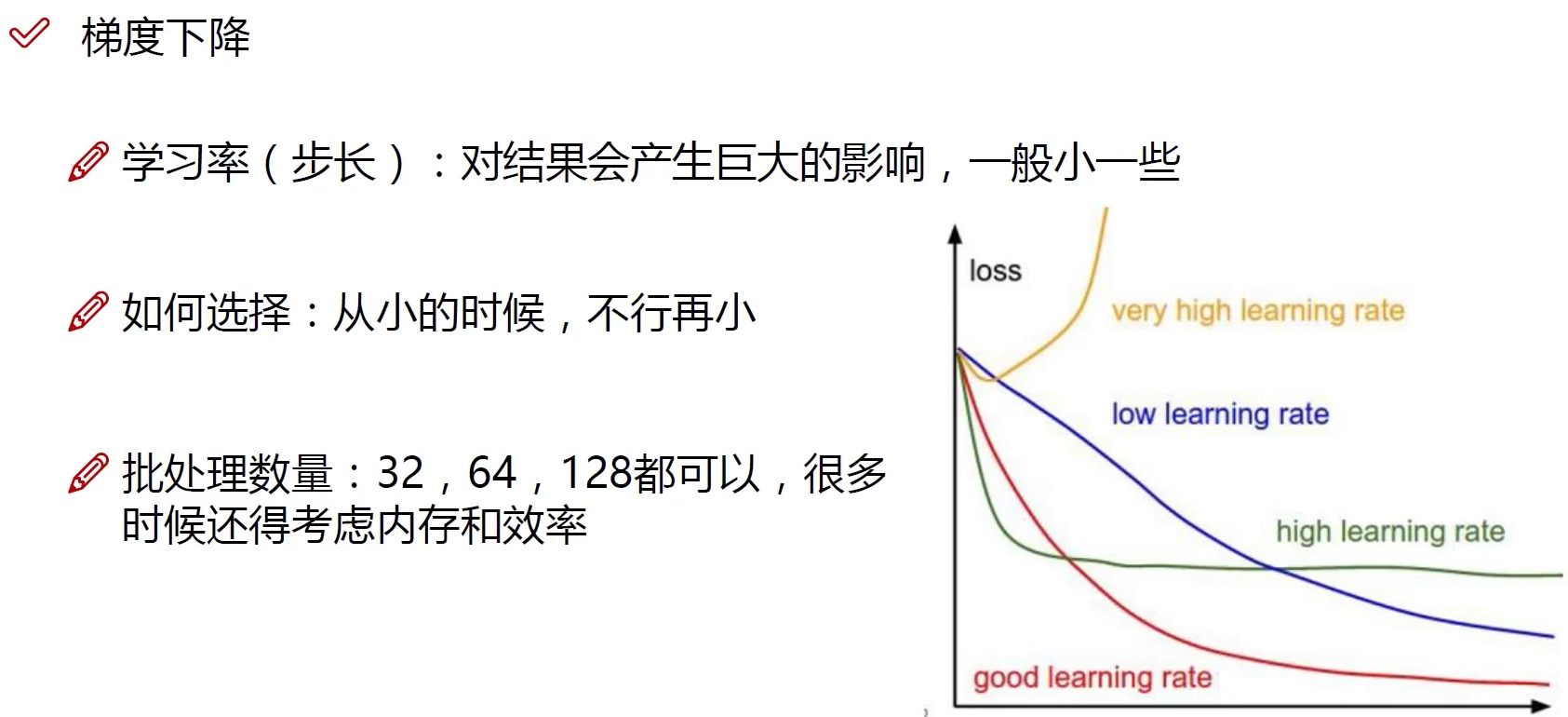
解释：

学习率小一点好些

下面是一个实例

UnivariateLinearRegression.py：（输入数据）

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

from linear_regression import LinearRegression

data = pd.read_csv('../data/world-happiness-report-2017.csv')

# 得到训练和测试数据
train_data = data.sample(frac=0.8)  # 从中选出80%的数据
test_data = data.drop(train_data.index)  # 把上面80%的数据弹出，返回剩下的20%
input_param_name = 'Economy..GDP.per.Capita.'
output_param_name = 'Happiness.Score'

x_train = train_data[[input_param_name]].values
y_train = train_data[[output_param_name]].values

x_test = test_data[input_param_name].values
y_test = test_data[output_param_name].values

plt.scatter(x_train, y_train, label='Train data')  # 创建散点图的点
plt.scatter(x_test, y_test, label='test data')  # 创建散点图的点
plt.xlabel(input_param_name)  # x轴
plt.ylabel(output_param_name)  # y轴
plt.title('Happy')  # 散点图的名字
plt.legend()  # 用于显示图例信息
plt.show()  # 显示图表本身。

num_iterations = 500    # 迭代次数
learning_rate = 0.01    # 学习率

linear_regression = LinearRegression(x_train, y_train)  # 进行预处理
(theta, cost_history) = linear_regression.train(learning_rate, num_iterations)  # 进行训练

print('开始时的损失：', cost_history[0])
print('训练后的损失：', cost_history[-1])

plt.plot(range(num_iterations), cost_history)   # 用于创建线性图并绘制损失的历史记录
plt.xlabel('Iter')  # x轴标签名字
plt.ylabel('cost')  # y轴标签名字
plt.title('GD')  # 图表名字
plt.show()  # 显示图表

predictions_num = 100   # 预测值
x_predictions = np.linspace(x_train.min(), x_train.max(), predictions_num).reshape(predictions_num, 1)  # 生成预测值所对应的输入参数
'''
linspace 是一个numpy库中用于生成等间距数值的函数。
start：序列的起始值
stop：序列的结束值
num：在起始值和结束值之间生成的等间距样本数量，默认值为50
'''
y_predictions = linear_regression.predict(x_predictions)  # 使用训练好的参数进行预测

plt.scatter(x_train, y_train, label='Train data')
plt.scatter(x_test, y_test, label='test data')
plt.plot(x_predictions, y_predictions, 'r', label='Prediction')  # 在散点图上绘制预测值，并设置其标签为“Prediction”，颜色为红色(看起来是一条线，其实是很多点)
plt.xlabel(input_param_name)
plt.ylabel(output_param_name)
plt.title('Happy')
plt.legend()
plt.show()

import numpy as np
from utils.features import prepare_for_training  # 导入预处理

class LinearRegression:

    def __init__(self, data, labels, polynomial_degree=0, sinusoid_degree=0, normalize_data=True):
        """
        初始化函数
        :param data: 原始数据矩阵，其中每行代表一个样本，每列代表一个特征（包括常数项）
        :param labels: 标签矩阵，其中每行代表一个样本的标签值
        :param polynomial_degree: 多项式回归的程度，默认为0，即不进行多项式回归
        :param sinusoid_degree: 正弦函数回归的程度，默认为0，即不进行正弦函数回归
        :param normalize_data: 是否进行数据规范化，默认为True，即进行规范化
        """
        # 对原始数据进行预处理，得到处理后的数据，以及平均值和偏差，用于数据规范化
        (data_processed,
         features_mean,
         features_deviation) = prepare_for_training(data, polynomial_degree, sinusoid_degree, normalize_data=True)

        self.data = data_processed  # 处理后的数据矩阵
        self.labels = labels  # 标签矩阵
        self.features_mean = features_mean  # 特征的平均值
        self.features_deviation = features_deviation  # 特征的偏差
        self.polynomial_degree = polynomial_degree  # 多项式回归的程度
        self.sinusoid_degree = sinusoid_degree  # 正弦函数回归的程度
        self.normalize_data = normalize_data  # 是否进行数据规范化
        num_features = self.data.shape[1]
        self.theta = np.zeros((num_features, 1))  # 参数矩阵，初始化为0

    def train(self, alpha, num_iterations=500):
        """
        训练函数，进行梯度下降
        :param alpha: 学习率
        :param num_iterations: 迭代次数，默认为500
        :return: 训练好的参数矩阵以及损失值列表
        """
        cost_history = self.gradient_descent(alpha, num_iterations)  # 执行梯度下降，得到损失值列表
        return self.theta, cost_history

    def gradient_descent(self, alpha, num_iterations):
        """
        梯度下降函数，进行实际的参数更新
        :param alpha: 学习率
        :param num_iterations: 迭代次数
        :return: 损失值列表
        """
        cost_history = []  # 损失值列表
        for _ in range(num_iterations):  # 迭代num_iterations次
            self.gradient_step(alpha)  # 进行一次参数更新
            cost_history.append(self.cost_function(self.data, self.labels))  # 计算当前训练集上的损失值，并加入损失值列表
        return cost_history

    def gradient_step(self, alpha):
        """
        参数更新函数，根据当前参数和学习率进行参数更新
        :param alpha: 学习率
        """
        num_examples = self.data.shape[0]  # 样本数
        prediction = LinearRegression.hypothesis(self.data, self.theta)  # 预测值
        delta = prediction - self.labels  # 预测值与真实标签的差距
        theta = self.theta  # 备份参数矩阵
        # 进行一次参数更新
        theta = theta - alpha * (1 / num_examples) * (np.dot(delta.T, self.data)).T     # 小批量梯度下降  delta.T 误差的转置乘于原始数据
        self.theta = theta  # 将更新后的参数赋值给参数矩阵

    def cost_function(self, data, labels):
        """
        损失函数，计算当前训练集上的损失值
        :param data: 数据矩阵
        :param labels: 标签矩阵
        :return: 当前训练集上的损失值
        """
        num_examples = data.shape[0]  # 样本数
        delta = LinearRegression.hypothesis(self.data, self.theta) - labels  # 预测值与真实标签的差距
        cost = (1 / 2) * np.dot(delta.T, delta) / num_examples  # 计算损失值
        return cost[0][0]

    @staticmethod
    def hypothesis(data, theta):
        """
        假设函数，计算预测值
        :param data: 数据矩阵
        :param theta: 参数矩阵
        :return: 预测值
        """
        predictions = np.dot(data, theta)  # 计算预测值
        return predictions

    def get_cost(self, data, labels):
        """
        获取某个数据集上的损失值
        :param data: 数据矩阵
        :param labels: 标签矩阵
        :return: 损失值
        """
        data_processed = prepare_for_training(data,
                                              self.polynomial_degree,
                                              self.sinusoid_degree,
                                              self.normalize_data
                                              )[0]
        return self.cost_function(data_processed, labels)

    def predict(self, data):
        """
        使用训练好的参数进行预测
        :param data: 数据矩阵
        :return: 预测值
        """
        data_processed = prepare_for_training(data,
                                              self.polynomial_degree,
                                              self.sinusoid_degree,
                                              self.normalize_data
                                              )[0]  # 对数据进行预处理
        predictions = LinearRegression.hypothesis(data_processed, self.theta)  # 计算预测值
        return predictions

'''
    1. 导入 numpy 和数据预处理函数 prepare_for_training
    2. 定义 LinearRegression 类，包括 init、train、gradient_descent、gradient_step、cost_function、hypothesis、get_cost、predict 方法
    3. 在 init 方法中，进行数据处理，包括调用 prepare_for_training 函数处理数据、初始化一些参数
    4. 在 train 方法中，调用 gradient_descent 函数进行梯度下降训练，返回训练好的参数矩阵和损失值列表
    5. 在 gradient_descent 方法中，进行 num_iterations 次迭代，每次迭代调用 gradient_step 函数更新参数，并计算损失值加入损失值列表
    6. 在 gradient_step 方法中，根据当前参数、学习率和预测值与标签之间的差距进行一次参数更新
    7. 在 cost_function 方法中，计算当前训练集上的损失值
    8. 在 hypothesis 方法中，计算预测值
    9. 在 get_cost 方法中，对数据进行预处理后计算对应的损失值
    10. 在 predict 方法中，对输入的数据进行预处理后使用训练好的参数进行预测
'''

写这个代码出现了几个问题：

from utils.features import prepare_for_training # 导入预处理 找不到这个包，这个包是私有的，得去网上下载
prepare_for_training () 不可以引用，解决方法:prepare_for_training.prepare_for_training(注意函数位置)

是引用里面的函数，不是这个py文件

报错

Traceback (most recent call last):
File "D:\AI\py\[demo1.py](http://demo1.py/)", line 35, in <module>
linear_regression = LinearRegression(x_train, y_train)
File "D:\AI\py\[main.py](http://main.py/)", line 19, in **init**
features_deviation) = prepare_for_training.prepare_for_training(data, polynomial_degree, sinusoid_degree,
File "D:\AI\py\utils\features\prepare_for_training.py", line 27, in prepare_for_training
) = normalize(data_processed)  # 执行标准化
File "D:\AI\py\utils\features\[normalize.py](http://normalize.py/)", line 30, in normalize
features_deviation[features_deviation == 0] = 1
TypeError: 'numpy.float64' object does not support item assignment

原因：train_data[input_param_name].values要改成train_data[[input_param_name]].values

因为里面还包了一层

画的图很密集，铺满整个画板，数据集太多了

plotly工具包，可以先到官网找模板，再改着用。

Plotly 是一个可以创建交互式可视化图表的 Python 库。它支持很多种类型的图表，例如散点图、线图、分布图、条形图、饼图、热力图等等。

模型评估

scikit-learn工具包

scikit-learn是一个开源的Python机器学习库，其主要提供了大量的常用机器学习算法和工具函数。其支持多种功能，包括数据预处理、特征提取、模型选择与评估、模型调优、数据挖掘、机器学习可视化等，并且对于常用的机器学习算法都有相应的实现。

scikit-learn的功能模块包括：

数据预处理模块（preprocessing）：包括标准化、归一化、缺失值填充、分类变量编码等。
特征提取模块（feature_extraction）：包括NLP中的文本特征提取、图像特征提取等。
监督学习模块（supervised_learning）：包括决策树、随机森林、SVM、朴素贝叶斯、线性回归、逻辑回归等。
无监督学习模块（unsupervised_learning）：包括聚类、主成分分析、降维等。
模型调参模块（model_selection）：包括交叉验证、网格搜索等。
数据集模块（datasets）：提供了一些常用的数据集供学习和测试使用。

sklearn数据集分为几种类型：

1、自带的小数据集（packaged dataset）：sklearn.datasets.load_

2、真实世界中的数据集（Downloaded Dataset）：sklearn.datasets.fetch_

3、计算机生成的数据集（Generated Dataset）：sklearn.datasets.make_

4、svmlight/libsvm格式的数据集:sklearn.datasets.load_svmlight_file(…)

5、从data.org在线下载获取的数据集:sklearn.datasets.fetch_mldata(…)

判断数据集文件放到哪里

from sklearn.datasets import get_data_home

# 获取默认数据集存储目录
data_home = get_data_home()

print("默认数据集存储目录：", data_home)

PIP的空间

机器学习

一些概念：

回归问题

1. 误差项定义

2. 独立同分布的意义

3. 似然函数的作用

4. 参数求解

5. 梯度下降

模型评估

scikit-learn工具包

你的赏识是我前进的动力